
Triangles are the most fundamental graphics primitive for drawing solid, 3D objects. Every complex object you see rendered (using rasterization techniques) is composed of a set of triangles, which may be modelled (i.e., composed by hand); or perhaps algorithmically, generated by mathematics and computer code.
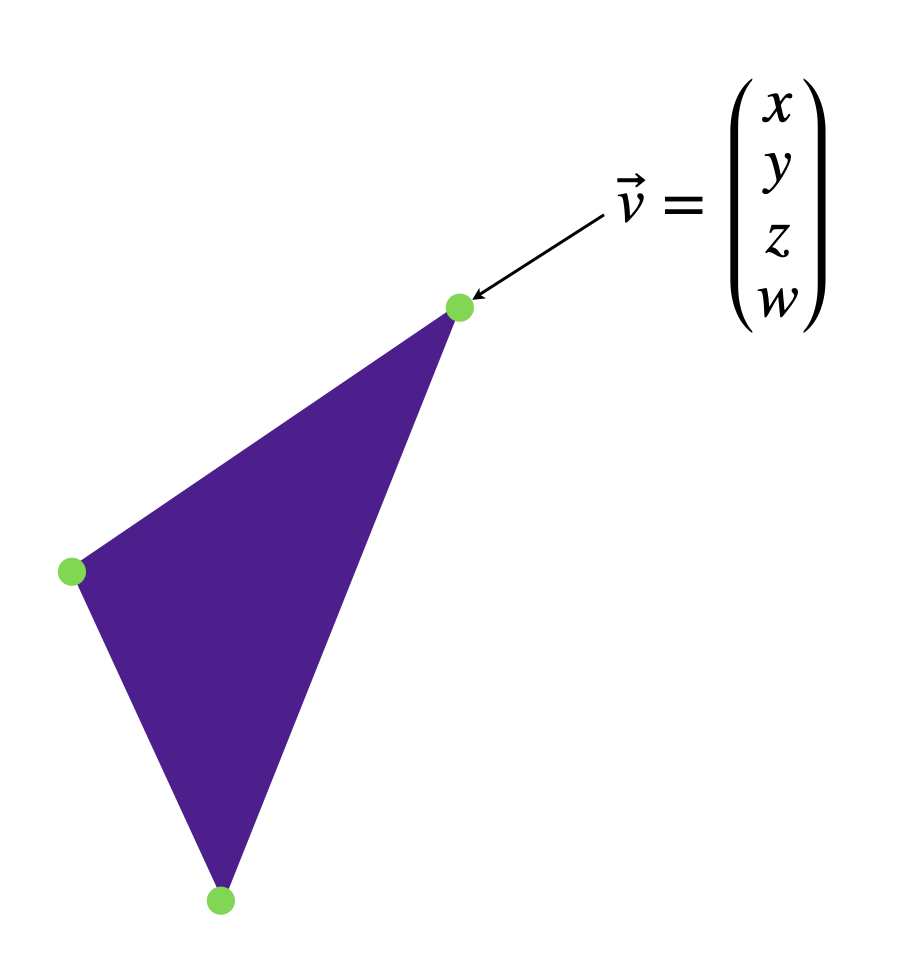
Regardless of the approach, triangles (and all computer graphics primitives) are specified by vertices. A vertex is a packet of information located at a point in space. While almost any information can be associated with a vertex, the one mandatory piece of information is its position. In 3D graphics, we specify positions using homogenous coordinates, which your normal \((x, y, z)\) positions in 3D space, and an extra coordinate (often called \(w\), which is pretty industry standard) which simplifies some of the math required for processing geometric primitives.
As you might expect, a triangle is specified by three vertices, that are usually unique (i.e., don’t have the same position. If two or more vertices are identical, you get what’s often called a degenerate triangle, and the system just ignores them).
The process of specifying vertices positions is called modeling, and sometimes you model each triangle individually, but most commonly, you’ll model a bunch of triangles that are connected, which means that triangles share vertices and edges. These are called connected primitives, and we’ll see more about them momentarily.

